TIL: Colliding Secure Hashes, FIFO and LRU Cache, GPS

Created in February 17, 2025

2025   ·   # TIL   # Cryptography   # Algorithm   # Systems

Colliding Secure Hashes

It’s interesting to see Pollard’s Rho Algorithm can be used in finding collision. Intuitively, this works because: the hash we try to break is a secure hash -> so it behaves like a PRF -> by the birthday paradox, we can find collisions in the same amount of time as naive birthday bruteforce algorithm.

parallel pollard's rho

The Parallel Pollard’s Rho method explores the time-space tradeoff (controlled by the distinguisher function) + parallelization. For a nn-bit hash and a distinguisher function enforcing the first kk-bit of the hash to be 0, a quick math gives us the following:

  • Space Complexity: O(2(n−k)2)O(2^{\frac{(n-k)}{2}}).
  • Time Complexity: O(2k∗2n−k2)O(2^k * 2^{\frac{n-k}{2}}).
  • As expected, the product of them is O(2n)O(2^n).

FIFO can be Better than LRU

Wonderfully simple ideas and very intuitive!

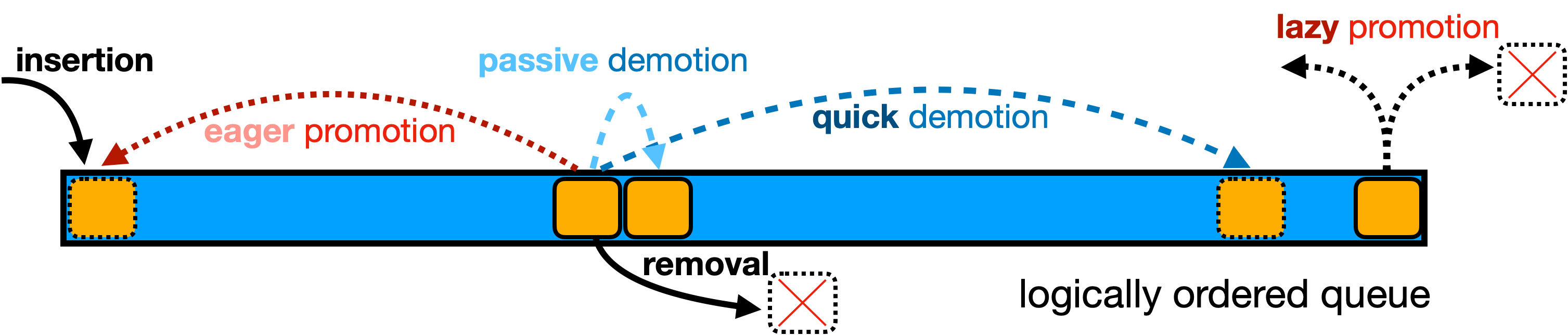
cache-abstraction
Cache Abstraction

Lazy Promotion

  • Their assumptions about popularity decay are basically in line with what I’ve encountered in real life.
  • Notably, this strategy also applies to the traditional LRU (simply replace eager promotion with lazy promotion). But, in such case, simply using FIFO is a much wiser choice.

Quick Demotion

  • Q: How to balance the size of the probationary FIFO queue? (parameter selection)
  • Q: Can we get more benefit by adding hierarchy (many FIFO queues with different sizes) to QD? What’s the tradeoff here?

GPS

An extremely well crafted articles discussing details about GPS. I particularly enjoy its visualizations a lot.

The authors cover a lot topics including

  • Trilateration on 2D plane
  • Time of Flight and Synchronization
  • Keplerian Elements
  • Inaccuracies
    • Time
    • Signal Propagation
  • Signal Processing and Coding

A few wonderful illustrations

(x−x1)2+(y−y1)2+(z−z1)2=v×(t1−b)(x−x2)2+(y−y2)2+(z−z2)2=v×(t2−b)(x−x3)2+(y−y3)2+(z−z3)2=v×(t3−b)(x−x4)2+(y−y4)2+(z−z4)2=v×(t4−b)\begin{aligned} \sqrt{(x - \textcolor{red}{x_1})^2 + (y - \textcolor{red}{y_1})^2 + (z - \textcolor{red}{z_1})^2} &= v \times (\textcolor{red}{t_1} - b) \\ \sqrt{(x - \textcolor{green}{x_2})^2 + (y - \textcolor{green}{y_2})^2 + (z - \textcolor{green}{z_2})^2} &= v \times (\textcolor{green}{t_2} - b) \\ \sqrt{(x - \textcolor{blue}{x_3})^2 + (y - \textcolor{blue}{y_3})^2 + (z - \textcolor{blue}{z_3})^2} &= v \times (\textcolor{blue}{t_3} - b) \\ \sqrt{(x - \textcolor{olive}{x_4})^2 + (y - \textcolor{olive}{y_4})^2 + (z - \textcolor{olive}{z_4})^2} &= v \times (\textcolor{olive}{t_4} - b) \end{aligned}

With this set of equations, we can solve for the x, y, and z coordinates of our position. But remember the complications: 1) how do we represent the coordinates of the satellites, 2) how do we calculate time of flight for satellite signal, 3) how can we successfully decode the signal, etc.

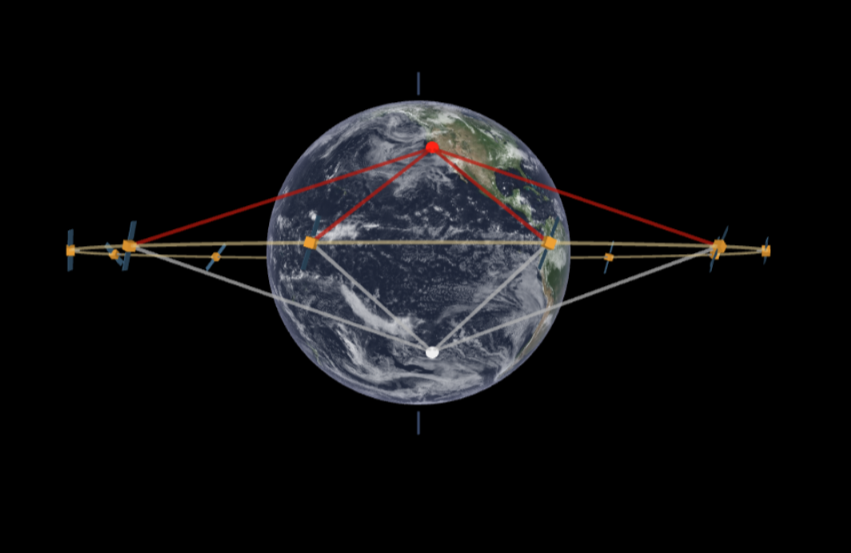
problem-of-geostationary-satellites
If all GPS satellites are geostationary, we cannot differentiate the north and south atmosphere.
problem-of-geostationary-satellites
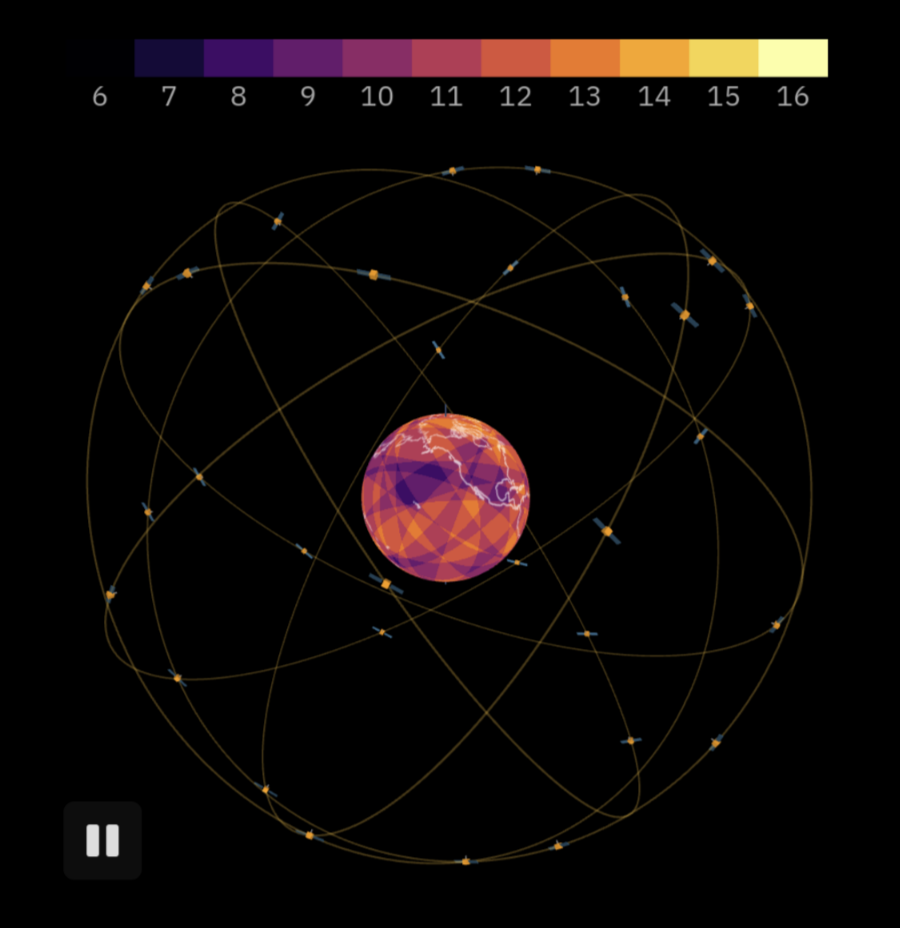
The number of visible satellites from every point on Earth, with density.
problem-of-geostationary-satellites
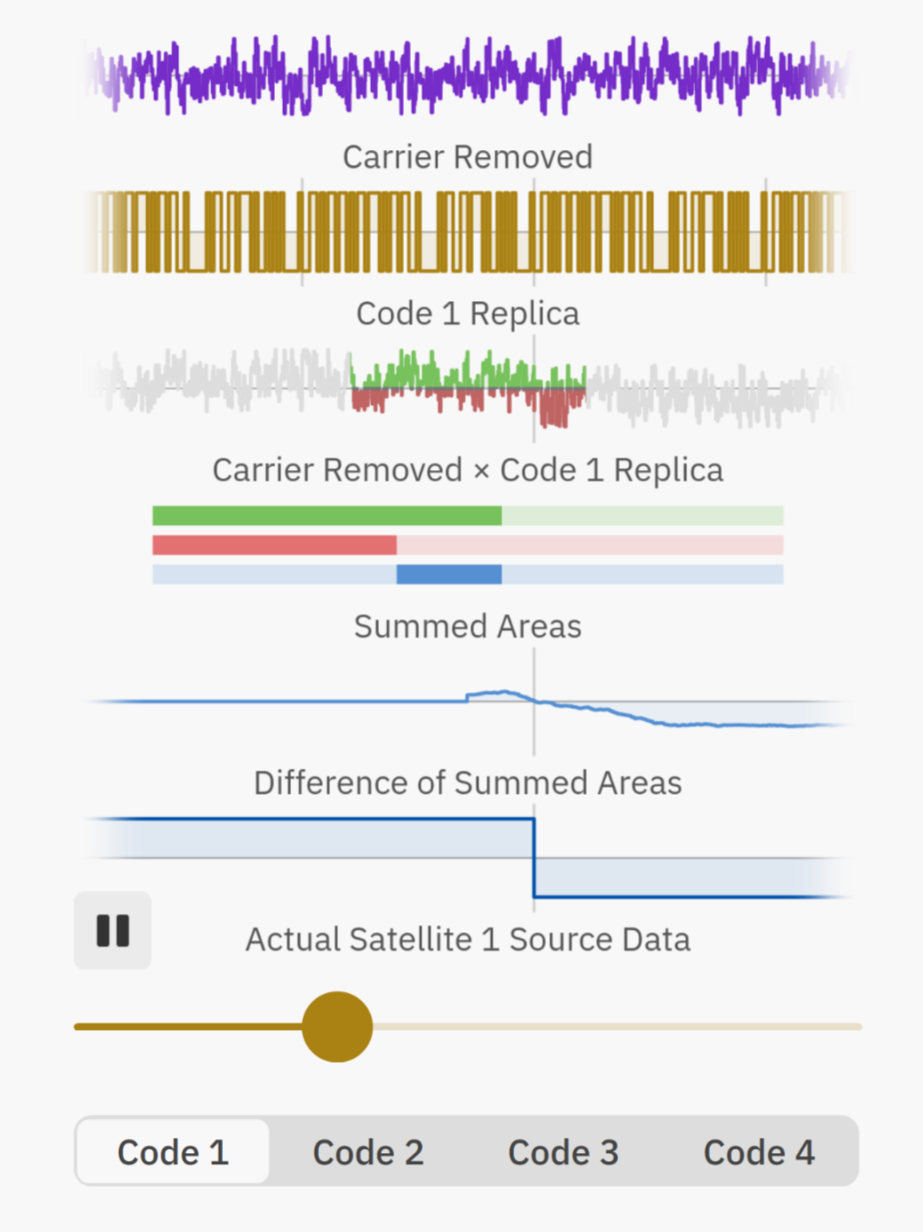
This shows how the signal is decoded. Since the code has high auto-correlation and low cross-correlation, we can decode the signal from the correct satellite.

Final Words

The final words are really touching:

It’s fascinating how much complexity and ingenuity is hidden behind the simple act of observing one’s location in a mapping app on a smartphone. What I find particularly remarkable is how many different technological advancements were needed for GPS to work.

Just the satellites themselves required the development of rockets, mastery of orbital controls, and manufacturing prowess to build devices capable of withstanding the extremes of space.

Precise time tracking was made possible by the invention of an atomic clock, while advancements in radio transmission and clever coding algorithms allowed the very weak signal sent by satellites to be correctly deciphered on Earth by receivers, which were in turn dependent on microchips and the digital revolution.

It’s hard not get inspired by the relentless drive of people who kept pushing science and technology forward. All of their work made GPS an indispensable tool in our everyday life.